1. The Structure of the Nucleon
Electromagnetic form factors (FFs) of the nucleon are the standard source of information on the internal structure of the nucleon, and as such have been studied extensively. The most recent generation of electron accelerators, which combine high current with high polarization electron beams, such as the Mainz Microtron (MAMI), MIT-Bates, or the Continuous Electron Beam Accelerator Facility (CEBAF) at Jefferson Lab (JLab), have made it possible to investigate the internal structure of the nucleon with unprecedented precision. In particular, the new generation of polarization experiments that make use of the target- and recoil-polarization techniques have allowed to chart the proton and neutron electromagnetic (e.m.) FFs very precisely.
Given the large amount of precise data on FFs it is of interest to exhibit directly the spatial information which results from these data. When viewing the nucleon from a light front moving towards the nucleon, a model independent 2-dimensional mapping of the quark charge density in the nucleon can be achieved in the transverse plane (perpendicular to the direction of motion). Using only the empirical information on the nucleon e.m. FFs, these transverse charge densities have been extracted [1] for an unpolarized nucleon, as well as for a transversely polarized nucleon, see Figure 1.

Figure 1: Quark transverse charge densities in the proton (left panels) and neutron (right panels), extracted from the empirical parameterizations of proton and neutron form factor data. The upper panel shows the density in the transverse plane for an unpolarized nucleon, whereas the lower panels show the density for a nucleon polarized along the x-axis. The light (dark) regions correspond with largest (smallest) values of the density. The lower panel compares the density along the y-axis for an unpolarized nucleon (dashed curve), and for a nucleon polarized along the x-axis (solid curve).
The aim of theoretical physics is not only to describe and interpret experimental data, but to make predictions for experimental results from theoretical considerations. The nucleon e.m. FFs have been calculated in the framework of a chiral effective theory [2]. In order to predict structural properties of hadrons, such as the nucleon FFs, from the underlying theory of the strong interactions (Quantum Chromodynamics, QCD), numerical simulations incorporating the full non-perturbative dynamics of QCD are required. Lattice QCD calculations of nucleon FFs have suffered for a long time from an insufficient control of the systematic uncertainties arising from the presence of excited states in the simulations. Recently, members of our group have published a study of the e.m. FFs of the nucleon [3] which incorporates full control of these uncertainties, as well as an improved approach to the uncertainties arising from the finite lattice spacing and unphysical pion mass used in the lattice simulations.
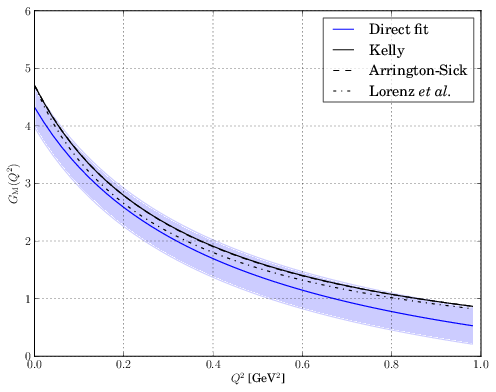
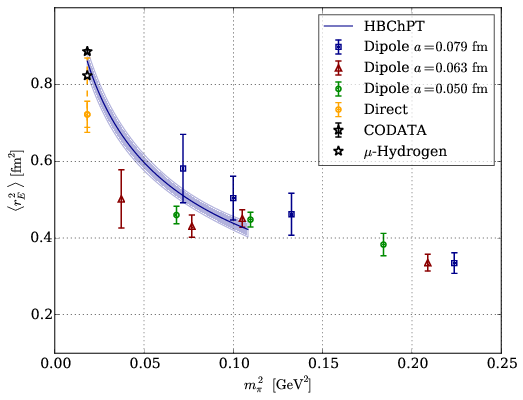
Figure 2: Left panel: the iso-vector magnetic form factor GM(Q2) of the nucleon as obtained from taking the continuum limit of lattice QCD simulations extrapolated to the physical pion mass (blue band) compared to three different parameterizations of the experimental data (black lines). Right panel: the iso-vector electric charge radius of the nucleon as obtained from lattice simulations at different values of the pion mass, with an extrapolation based on Heavy-Baryon Chiral Perturbation Theory (HBChPT) compared to the experimental results from ep scattering (CODATA) and muonic hydrogen spectroscopy.
Given the precision of the existing information on the structure of the nucleon, it came as a surprise when an independent measurement of the electric charge radius of the proton using the spectroscopy of muonic hydrogen gave a value that disagreed with the e.m. FF measurements by several standard deviations. This so-called proton radius puzzle could be a first sign of new low-energy physics, or an indication of a gap in our understanding of QCD. Mainz theorists have pointed out that even a small non-monotonicity in the electric form factor at small momentum transfer, whatever its underlying cause, could be enough to reconcile the existing proton radius measurements [4].
The nucleon e.m. FFs access the quark-gluon structure of the nucleon by measuring the matrix element of a well-defined quark-gluon operator (in this case the vector operator ̅̅qγνq) over the hadronic state. One is however not limited in nature to probes such as photons (or W, Z bosons for the axial transition). The phenomenon of asymptotic freedom of QCD, meaning that at short distances the interactions between quarks and gluons become weak, provides us with more sophisticated QCD operators to explore the structure of hadrons. Such operators can be accessed by selecting a small-size configuration of quarks and gluons, provided by a hard reaction, such as deep inelastic scattering (DIS), or hard exclusive reactions such as deeply virtual Compton scattering (DVCS), γ*(qh) + N(p) → γ (q') + N(p'), where the virtual photon momentum qh is the hard scale. The common important feature of such hard reactions is the possibility to separate clearly the perturbative and non-perturbative stages of the interactions: this is the so-called factorization property. The non-perturbative stage of such hard exclusive electroproduction processes is described by universal objects, so-called generalized parton distributions (GPDs) [5].
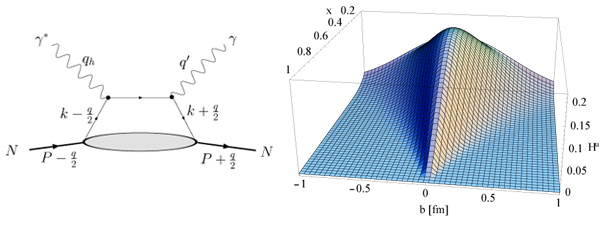
Figure 3: Left panel: handbag diagram for the nucleon DVCS process. Provided the virtuality of the initial photon (with momentum qh) is sufficiently large, the QCD factorization theorem allows to express the total amplitude as the convolution of a Compton process at the quark level and a non-perturbative amplitude parameterized in terms of GPDs (lower blob). Right panel: the GPD Hu for a valence up-quark in the proton as function of the quark momentum fraction x and the quark position b in the transverse plane (perpendicular to the average direction of the fast moving nucleons). The calculation is based on the 3-parameter modified Regge parametrization for the GPDs.
These GPDs have the physical meaning of measuring the probability to find a quark which carries longitudinal momentum fraction x at a transverse position b⊥ (relative to the transverse center-of-momentum) in a nucleon, and are related both to form factors and to more general object such as generalized transverse-momentum dependent parton distributions (GTMDs) [6].
References:
[1] C.E. Carlson and M. Vanderhaeghen, Phys. Rev. Lett. 100 (2008) 032004; arXiv:0807.4537 [hep-ph].[2] T. Bauer, J.C. Bernauer and S. Scherer, Phys. Rev. C86 (2012) 065206; arXiv:1209.3872 [nucl-th].
[3] S. Capitani, M. Della Morte, D. Djukanovic, G. von Hippel, J. Hua, B. Jäger, B. Knippschild, H.B. Meyer, T.D. Rae and H. Wittig, Phys. Rev. D92 (2015) 054511; arXiv:1504.04628 [hep-lat].
[4] F. Hagelstein and V. Pascalutsa, Phys. Rev. A91 (2015) 040502; arXiv:1502.03721 [hep-ph].
[5] M. Boër, M. Guidal, M. Vanderhaeghen, Eur. Phys. J. A51 (2015) 103.
[6] C. Lorcé, B. Pasquini, M. Vanderhaeghen, JHEP 1105 (2011) 041; arXiv:1102.4704 [hep-ph].
2. The Anomalous Magnetic Moment of the Muon
The most promising sign of possible new physics at the moment is the discrepancy between the anomalous magnetic moment of the muon as theoretically calculated within the Standard Model (SM) of elementary particle physics and as measured in high-precision experiments. While both determinations are accurate to less than a part per million, they differ at the level of two to three standard deviations (>2σ). To ascertain whether this discrepancy is really an indication of new physics, all uncertainties in the theoretical determination must be brought under control; the leading source of theoretical uncertainty lies in hadronic effects, such as the hadronic vacuum polarization (HVP) and the hadronic light-by-light (HLbL) scattering cross-section.
The HVP describes how the presence of the strong interactions modifies the electromagnetic interactions at short distances; through the unitarity and analyticity of the S-matrix, it can be related to the cross-section for the production hadronic final states in e+e- annihilation, which is known from experiment. For a theoretical determination from first principles, the correlation function of two electromagnetic currents needs to be measured in lattice QCD. The difficulty of resolving the low-energy region, which needs to be known precisely in order to determine the HVP contribution to the anomalous magnetic moment of the muon with an accuracy relevant to phenomenology can be addressed with a variety of theoretical tools, such as twisted boundary conditions [1] or a mixed time-momentum representation [2].
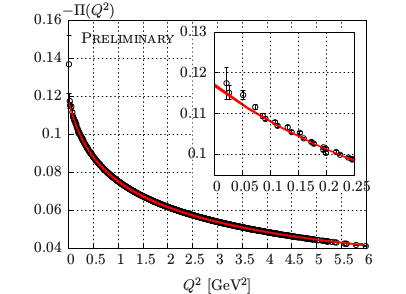
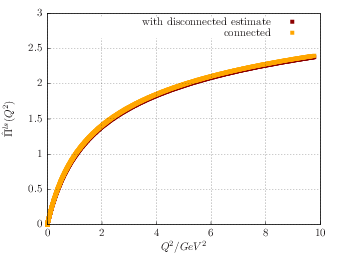
Figure 4: Left panel: the hadronic vacuum polarization function from lattice QCD using twisted boundary conditions; the inset indicated the concentration of points in the low-momentum region possible using this technique. Right panel: using the time-momentum representation, the subtracted vacuum polarization function can be obtained directly as a continuous function of momentum; the red curve indicates an estimate of the effect of quark-disconnected diagrams.
The HLbL cross-section is not directly accessible to experiment, but efforts have been made to determine it from dispersion relations in a similar manner to the phenomenological determination of the HVP [3]. When combined with hadronic models, a theoretical estimation of the HLbL contribution to the anomalouse magnetic moment is possible [4]. In a ground-breaking study, Mainz theorists have explicitly calculated the hadronic light-by-light scattering amplitude from first principles in lattice QCD [5]. The results indicate that hadronic models are reliable at least in the region of forward photon-photon scattering.
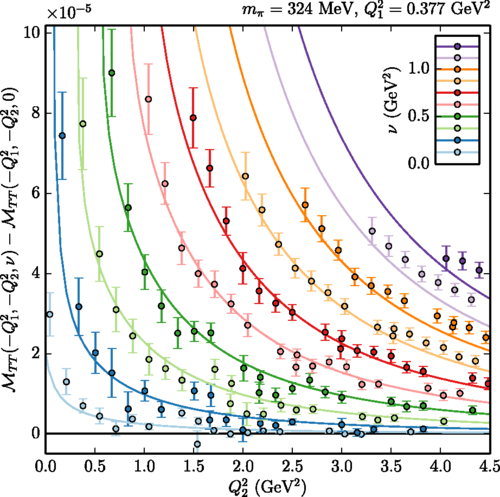
Figure 5: Comparison between the results for the forward scattering amplitude ℳTT for hadronic light-by-light scattering at fixed virtuality Q12=0.377 GeV2 as a function of the virtuality Q22 of the other photon for different values of the invariant ν. Data points are obtained from a direct lattice QCD simulation, whereas the curves are a prediction from a dispersive sum rule in conjunction with a phenomenological hadronic model for the transverse cross section for γ*γ* → hadrons.
References:
[1] M. Della Morte, B. Jäger, A. Jüttner, H. Wittig, JHEP 1203 (2012) 055; arXiv:1112.2894 [hep-lat].[2] A. Francis, B. Jäger, H. B. Meyer, H. Wittig, Phys.Rev. D88 (2013) 054502; arXiv:1306.2532 [hep-lat].
[3] V. Pauk, M. Vanderhaeghen, Phys. Rev. D90 (2014) 113012; arXiv:1409.0819 [hep-ph].
[4] P. Masjuan, M. Vanderhaeghen, J. Phys. G42 (2015) 125004; arXiv:1212.0357 [hep-ph].
[5] J. Green, O. Gryniuk, G. von Hippel, V. Pascalutsa, H. B. Meyer, Phys. Rev. Lett. 115 (2015) 222003; arXiv:1507.01577 [hep-lat].
[6] F. Hagelstein, V. Pascalutsa, Phys.Rev.Lett. 120 (2018) 072002; arXiv:1710.04571 [hep-ph].
3. Dynamics and Properties of Light Mesons
The dynamics of the lightest mesons is described by chiral perturbation theory, which in its simplest form is a theory of pions acting as quasi-Goldstone bosons for the spontaneously broken approximate chiral symmetry of QCD. It is possible to systematically extend chiral perturbation theory in order to include vector mesons [1] as well as baryons [2], and the Mainz group maintains its position at the forefront of such efforts, as evidenced by the review articles and textbooks [3] on this topic written by group members.
Many of our activities on the lattice side are also closely related to chiral perturbation theory, in particular to the determination of its low-energy constants from first principles. As an example, the low-energy constant ̅̅l4 has been determined precisely from measurements of the scalar form factor of the pion in lattice QCD [4], which required the inclusion of quark-disconnected diagrams incorporating explicit sea-quark contributions to the form factor.
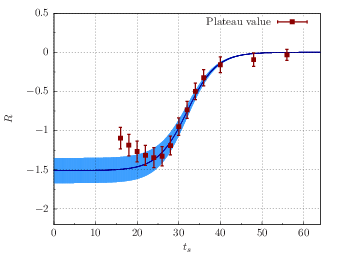
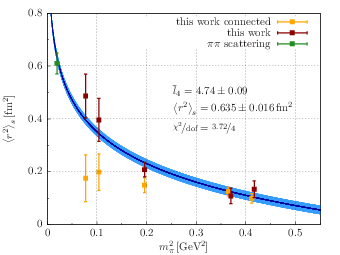
Figure 6: Left panel: extracting the quark-disconnected contribution to the scalar form factor of the pion from lattice QCD; the blue band represents a one-parameter fit to the data shown in red, corresponding to extracting the value of the form factor at a given momentum transfer from a ratio of Euclidean correlation functions. Right panel: the scalar radius as a function of the pion mass together with a one-parameter fit to the prediction from Chiral Perturbation Theory, with the phenomenological value extracted from ππ scattering (shown in green) for comparison; it can be seen that only the complete (connected plus disconnected) results (shown in red) agree with the shape predicted by ChPT, which the results incorporating only connected contributions (shown in yellow) cannot replicate.
References:
[1] D. Djukanovic, J. Gegelia, S. Scherer, Int. J. Mod. Phys. A25 (2010) 3603; arXiv:1001.1077 [hep-th].[2] S. Scherer, J. Phys. Conf. Ser. 348 (2012) 012001; arXiv:1112.5600 [hep-ph].
[3] S. Scherer, M. Schindler, A Primer for Chiral Perturbation Theory, Lecture Notes in Physics, Vol. 830 (Heidelberg:Springer, 2012).
[4] V. Gülpers, G. von Hippel, H. Wittig, Eur. Phys. J. A51 (2015) 158; arXiv:1507.01749 [hep-lat].
4. Nuclear Structure Corrections in Muonic Atoms
Atomic spectra can be quite well explained by considering the dynamics of leptons orbiting around a point–like nucleus. However, when precision is required, one has to consider that the nucleus has both a finite size and a compound nature. In hydrogen–like muonic atoms—systems where a muon orbits a nucleus—the muon is much closer to the nucleus than an electron, owing to its heavier mass. Consequently, nuclear structure effects become important and need to be well understood.
In laser spectroscopy on muonic atoms, which has proven to be a tremendous tool to measure nuclear radii, the knowledge of nuclear structure effects constitutes the main bottleneck to fully exploit the experimental precision. Using chiral effective field theory and state-of-the-art few-body methods we have recently computed such corrections with a precision of the order of a few-precent [1-5], superseding previous estimates and providing thereby an instrumental contribution to the success of the muonic atom program.
Our most recent achievement is the development of a hybrid theoretical approach in which we first perform chiral effective field theory computations of electromagnetic response functions and then use the latter to inform the dispersion relation method and compute nuclear structure corrections. In a recent joint paper [6], coauthored by 5 Mainz theorists, we showed that this approach is successful for (muonic) deuterium, see Figure 1. Using a combination of theory and experiment to inform dispersion relations opens up the possibility to improve the attainable precision also for other light nuclei.
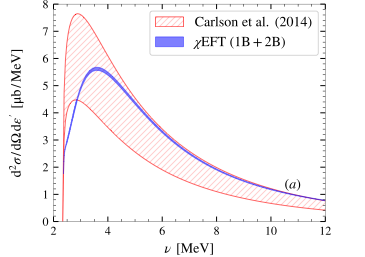
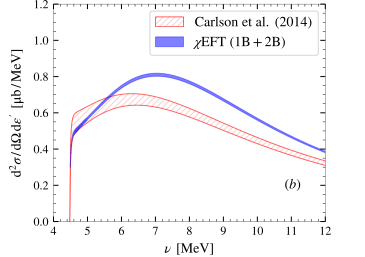
Figure 7: Electro-dissociation cross section of the deuteron: comparison of the χEFT calculation (blue band) with the dispersion relation results by Carlson et al (hatched red band) at energy/angle (a) ε = 80 MeV, θ = 16° and (b) ε = 180 MeV, θ = 30°.
References:
[1] C. Ji, N. Nevo Dinur, S. Bacca, N. Barnea, Phys. Rev. Lett. 111 (2013) 143402; arXiv:1307.6577[2] N. Nevo Dinur, C. Ji, S. Bacca, and N. Barnea, Physics Letters B 755 (2016) 380-386; arXiv:1512.05773
[3] C. Ji, S. Bacca, N. Barnea, O.J. Hernandez, N. Nevo Dinur, J. Phys. G 45 (2018) 093002; arXiv:1806.03101
[4] O.J. Hernandez, A. Ekstrom, N. Nevo Dinur, C. Ji, S. Bacca, and N. Barnea, Phys. Lett. B 778 (2018) 377-383; arXiv:1711.01199
[5] O.J. Hernandez, C. Ji, S. Bacca, N. Barnea, Phys. Rev. C 100 (2019) 064315 (2019); arXiv:1909.05717
[6] B. Acharya, V. Lensky, S. Bacca, M. Gorchtein, and M. Vanderhaeghen, Phys. Rev. C 103 (2021) 024001; arXiv:2010.11155